「確率の収束」「試行回数」とは何か? 簡単な例付きで解説
さて,今回はパチンコ・パチスロで時折見かける
「確率の収束」だとか「試行回数」について
実例を使って,できるだけ簡単に解説しようと思います.
専門的なことや,ダラダラとした数式は控えめなので,お気軽に読んで下さいね~
期待値について知りたい方は,こちら見てください
「期待値」とは何か? 簡単な例付きで解説
収束の意味
「確率が収束する」ってどういう意味?
と疑問に感じていらっしゃる方も,世の中にはいると思います.
まぁでも実際はそんなにややこしいものではなくて
ザックリ言ってしまえば
「ある事が起こる確率が,理論通りの数値に近づく」
たったこれだけなんですね~
あと,この確率の収束を説明する上で,どうしても外せないキーワードがあります.
それが,「試行回数」ですね.
これはそのままの意味で
「ある事について試してみる回数」
ということですね,では解説を始めます.
収束の例
今回は収束の例として,誰でも容易に想像ができる…
「サイコロ」を使いましょう!
さて,このサイコロに何の仕掛けもない時に
「1~6の各出目が出現する確率は?」
と,聞かれたとします.
何の意地悪もないですよ?
答えはもちろん
「全ての目が等しく1/6である」ですよね.
これがいわゆる「理論通りの値」になります.
では実際に振ったらどうなるのか…?
本当に1/6になるのか?
まぁこういった疑問を持つのも当然ですよね.
実際にやってみた
さて,実際にやってみるわけなのですが…
残念ながら今僕の手元にはサイコロはありません.
しかも確率の収束にはかなり多くの試行回数が必要です.
というわけで…エクセルのRAND関数を使います!
RAND関数とは?
こんなワードを急に出しても「?」となるだけでしょう.
しかし,これはとても簡単に使えるエクセルの機能です.
0以上で1より小さい乱数を発生させます。ワークシートが再計算されるたびに、新しい乱数が返されます。
引用:Excel(エクセル)基本講座:ランダムな数値を返す関数(RAND関数、RANDBETWEEN関数)
ザックリ言うと
「0以上1未満の数字をランダムに表示する」
ってことです.
実際に使うとこうなります
| RAND関数 |
|---|
| 0.76369576 |
| 0.359534593 |
| 0.74025522 |
この乱数を
「0以上1未満の数字を6つのグループに分ける」
ことによって,擬似的にサイコロを実現します.
今度こそやってみた
さて,RAND関数の説明も済んだところで,実際にやってみましょう
今回は試行回数N(サイコロを振る回数)を
20,50,100,200,500,1000,5000,10000回として
それぞれの場合の各出目の出現率を求めます.
数値は[%]として出力します.
つまり各出目の出現率が1/6=16.6666・・・[%]
に近くなれば,実践値が理論値に近づいた
つまり「確率が収束した」ということになります.
結果は以下の通りになりました
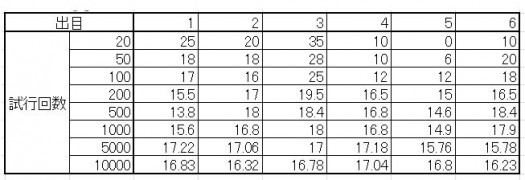
結局,理論値との一致とまではなりませんでしたが…
試行回数を重ねるごとに,理論値へ近づいている様子が確認できます
これが,「確率の収束」です.
まとめ
今回も例を使って,ザックリと色々説明しましたが…
とにかく言いたいことは
「回数を重ねれば重ねるほど,理論通りの結果に近づく」
ということです.
確率が1/6程度のサイコロでさえ,これだけ収束しづらいのですから.
スロットとなると,もっともっと収束しづらいことは事実です.
しかし,すぐに収束しないからこそ
「平打ちをしばらく続けても,勝てることがある」わけですね.
これ,勝つためにはダメな例ですね.
収束しづらいとはいえ,ある程度の試行回数でも
それなりに確率の傾向が見えてくることは確かです.
これは言い換えれば
「高時給ボーダーを打ち続ければ,個人差はあるもののまず負けない」
ということでもあります.
結局,ずっと打ってりゃ勝てるってことなんですけど…
現実には資金切れなどで機会を失ったりすることもあるわけです.
勝てることは事実です,そこは疑わなくて良いと思います.
しかし,それ以外の面でも考慮できなければなりません.
これからはそういった趣旨の記事も書いていこうと思います~

コメント一覧
なんだっけな、完全に収束させる事は理論上不可能だからの収束だっけか。
んでも、良く勘違いがあると思うんだけど、俺のアフロの勘違い②みたいな。
まぁ,偶然の一致があり得たとしても
何事に対しても上ブレもなく下フレもなく収束するなら,世界がヤバそうですw
URL埋め込んどきました☆
こんばんはー(*´ω`*)
にゃりの師匠もそんなこと
言っていたきがします!
確かにですねー
お勉強になりましたー!
ぽち☆
どもども~
にゃりねーの師匠さんは,ちゃんと確率論を理解してらっしゃるんですね(・∀・)
良い師だと思います.
理解の助けに慣れれば幸いですー
応援感謝です!
おはようございます(*´ω`*)
にゃりの師匠はSEで
数字にめっちゃ強いのです。
ヒキは弱いかな?w
じょんぷさんのブログ
良くできてるって言って、見てますよ~
SEさんですか!
そりゃ強いでしょうね(°∀°)
まだまだガキの稚拙なものですが、評価頂けるのは嬉しいですね♪
1万回、サイコロ振っても、結構バラつきはあるんですね。
10万回いけば、ピッタリな数字でるのかな?
10万回振ってみると,かなり安定してきましたね~
しかしこの「10万回振る」という行為自体にもバラツキがあるので「完全な収束」なんてことは実はありえなかったりしますね.
しかし「限りなく現実が理論に近づく」わけです.
あ〜はいはい サウンドエフェクトね(・∀・)はいはいはいはい わかるわかる
北斗のぴき〜とかやね
(゚∀゚)…
(絶対この人分かってて言ってるよー)
(°∀°)…
(だって俺就職した時職種SEなるかcustomerの方にいくかだったもん…)
やっぱりw
( ´゚д゚)(゚д゚` )ネー
ハイエナ始めて下ブレした人こそ知っておく内容だね〜
上にブレた人は良いけど下ブレすると数こなす前に嫌になるからね
そうですねー
でも上ブレの人も知っておいて欲しいですね.
平打ち勢からの転身組なら,勘違いしてボーダー緩めたりするかもですし…
わかりやすい。
じょんぷさん計算つよいよね。
自分は文系なので算数程度の知識が一向に伸びませんw
そう思っていただけたなら良かったです♪
まぁ…一応理数系の学生ですからねー
こういう確率論は計算する能力というより「どうやったら求められるか」といった「方法」を知るものですからね~
あと,知っていて損は絶対にないですけど,体感的に理解して,実践できているのであれば実質は必要ないですかね.
「稼働がうまく行かなかった時の言い訳」程度にしておきましょうw
8000Gあれば多少は
収束するのかな、て感覚はありますね。
たまに今まで〜だから
収束して〜に向かっていくみたいな
勘違いする人もいますけどw
まぁたいていの設定判別などはそれくらいでも傾向は見えたりするんだと思います。
各小役の確率まで、っていうとなかなか難しいでしょうけど…
その勘違いが発展して、「出るときから出なくなるときまでの流れ」を「波」と勘違いして、意味不明な読みが始まるんですねー
[…] 「確率の収束」「試行回数」とは何か? 簡単な例付きで解説 「引き」「波」「相性」について考察 引用元 じょんぷのエナスロ! […]
こんばんは~
面白い記事ですね!
私はゲーセンでビッグ確率が1/240の台(設定6)をいつも打っています。
だいたい半日回して4000Gくらいで切り上げるのですが、良い方にぶれるときは『1/140』、悪い方にぶれるときは『1/360』の確率でした。
感覚的には、数万ゲーム回せば、ある程度収束しそうな感じがします。
コメントありがとうございます!
ゲーセンのスロットも時々打ちますけど…4000Gはすごいですねw
もう実機買っちゃいましょうよ(・∀・)
数万ゲームですか…ちょうどGODを23000Gくらい回した記事も書いてますよw
【稼働日記】3日間GOD凱旋ツッパ生活 ~絶望の始まり~【1日目 前編】